Swift数据结构和算法（一）

Posted on Edited on

第一部分：引言

第一章：前言

数据结构是一门经过充分研究的学科，其概念与语言无关; 来自C的数据结构在功能上和概念上与任何其他语言中的相同数据结构相同，例如Swift。 与此同时，Swift的高级表现力使其成为学习这些核心概念的理想选择，而不会牺牲太多的性能。

Swift标准库有一小组通用集合类型; 他们甚至没有涵盖每一个案例。正如您将看到的，这些 原始的类型可以用作构建更复杂和特殊用途构造的一个很好的起点。 了解比标准数组和字典更多的数据结构，您可以使用更多的工具来构建自己的应用程序。

第二章：Swift标准库

在开始构建自己的自定义数据结构之前，了解Swift标准库已经提供的主要数据结构非常重要。

字典缺乏明确的排序劣势，却又带来了一些其他的优点。 与数组不同，字典不需要担心元素的转移。 插入字典总是O(1)。 查找操作也在O(1)时间内完成，这比在需要O(n)扫描的数组中找到特定元素要快得多。

第三章：复杂度

常见的时间复杂度和空间复杂度。

对于计算机，算法的资源是内存。空间复杂度就意味着内存占用率。

总结

  • 时间复杂度衡量输入大小增加时运行算法所需的时间。

  • 空间复杂度衡量算法运行所需的资源。

  • Big O表示法用于表示时间和空间复杂性的一般形式。

  • 时间和空间复杂性是可扩展性的高级度量; 它们不测量算法本身的实际速度。

  • 对于小型数据集，时间复杂度通常无关紧要。 拟线性算法可能比线性算法慢。

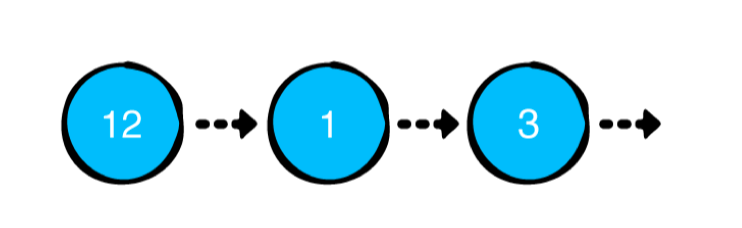
第二部分：基本数据类型

第四章：链表

链表是以线性单向序列排列的值的集合。链表比连续存储选项（如Swift数组）具有几个理论上的优势：

  • 从列表前面插入和删除恒定时间。
  • 可靠的性能特征。

image-20190801154442688

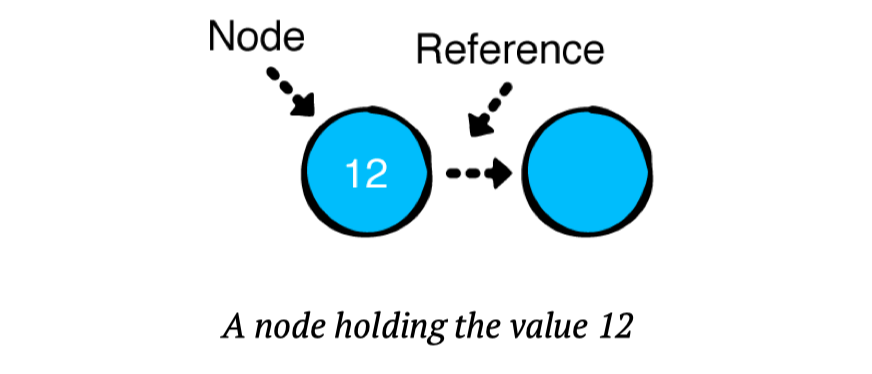
如图所示，链表是一系列节点。 节点有两个职责：

1.保存一个值。

2.保存对下一个节点的引用。 空表示列表的结尾。image-20190801154554314

节点

1
2
3
4
5
6
7
8
9
10
public class Node<Value> {
  
  public var value: Value
  public var next: Node?
  
  public init(value: Value, next: Node? = nil) {
    self.value = value
    self.next = next
  }
}

链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
public struct LinkedList<Value> {
  
  public var head: Node<Value>?
  public var tail: Node<Value>?
  
  public init() {}
  
  public var isEmpty: Bool {
    return head == nil
  }
  
  // MARK: - 增加和删除节点的方法
  
  // 时间复杂度：O(1)
  public mutating func push(_ value: Value) {
    copyNodes()
    head = Node(value: value, next: head)
    if tail == nil {
      tail = head
    }
  }

  // 时间复杂度：O(1)
  public mutating func append(_ value: Value) {
    copyNodes()
    guard !isEmpty else {
      push(value)
      return
    }
    tail!.next = Node(value: value)
    tail = tail!.next
  }

  // 时间复杂度：O(i) , i 就是给定的index
  public func node(at index: Int) -> Node<Value>? {
    var currentNode = head
    var currentIndex = 0
    while currentNode != nil && currentIndex < index {
      currentNode = currentNode!.next
      currentIndex += 1
    }
    return currentNode
  }
  
  // 时间复杂度：O(1)
  @discardableResult
  public mutating func insert(_ value: Value, after node: Node<Value>) -> Node<Value> {
    copyNodes()
    guard tail !== node else {
      append(value)
      return tail!
    }
    node.next = Node(value: value, next: node.next)
    return node.next!
  }

  // 时间复杂度：O(1)  
  @discardableResult
  public mutating func pop() -> Value? {
    copyNodes()
    defer {
      head = head?.next
      if isEmpty {
        tail = nil
      }
    }
    return head?.value
  }
  
  // 时间复杂度：O(n)
  @discardableResult
  public mutating func removeLast() -> Value? {
    copyNodes()
    guard let head = head else {
      return nil
    }
    guard head.next != nil else {
      return pop()
    }
    var prev = head
    var current = head
    while let next = current.next {
      prev = current
      current = next
    }
    prev.next = nil
    tail = prev
    return current.value
  }

  // 时间复杂度：O(1)  
  @discardableResult
  public mutating func remove(after node: Node<Value>) -> Value? {
    copyNodes()
    defer {
      if node.next === tail {
        tail = node
      }
      node.next = node.next?.next
    }
    return node.next?.value
  }

  // MARK: - 实现值类型和写入时复制
  //使用COW实现价值语义的策略非常简单。在改变链接列表的内容之前，您希望执行底层存储的副本并将所有引用（头部和尾部）更新为新副本。
  private mutating func copyNodes() {
    guard !isKnownUniquelyReferenced(&head) else {
      return
    }
    guard var oldNode = head else {
      return
    }
    
    head = Node(value: oldNode.value)
    var newNode = head
    
    while let nextOldNode = oldNode.next {
      newNode!.next = Node(value: nextOldNode.value)
      newNode = newNode!.next
      oldNode = nextOldNode
    }
    
    tail = newNode
  }
}

// MARK: - 实现Swift的Collection协议

//Swift Collection还允许通过下标进行访问，这是一个很好的术语，用于表示索引可以映射到集合中的值。
extension LinkedList: Collection {
  
  public struct Index: Comparable {
    
    public var node: Node<Value>?
    
    static public func ==(lhs: Index, rhs: Index) -> Bool {
      switch (lhs.node, rhs.node) {
      case let (left?, right?):
        return left.next === right.next
      case (nil, nil):
        return true
      default:
        return false
      }
    }
    
    static public func <(lhs: Index, rhs: Index) -> Bool {
      guard lhs != rhs else {
        return false
      }
      let nodes = sequence(first: lhs.node) { $0?.next }
      return nodes.contains { $0 === rhs.node }
    }
  }
  
  public var startIndex: Index {
    return Index(node: head)
  }
  
  public var endIndex: Index {
    return Index(node: tail?.next)
  }
  
  public func index(after i: Index) -> Index {
    return Index(node: i.node?.next)
  }
  
  public subscript(position: Index) -> Value {
    return position.node!.value
  }
}

关键点

  • 链接列表是线性和单向的。 只要将引用从一个节点移动到另一个节点，就无法返回。
  • 链接列表的头部第一次插入具有O(1)时间复杂度。 对于头部第一次插入，数组有O(n)时间复杂度。
  • 符合Swift收集协议（如序列和集合），可为相当少的要求提供一系列有用的方法。
  • 写时复制行为使您可以实现值语义。

第五章：链表挑战

逆序打印所有节点元素

1
2
3
4
5
6
7
8
9
10
func printInReverse<T>(_ list: LinkedList<T>) {
  //巧妙的递归：先迭代后打印，这样打印的就是逆序了
  printInReverse(list.head)
}

private func printInReverse<T>(_ node: Node<T>?) {
  guard let node = node else { return }
  printInReverse(node.next)
  print(node.value)
}

取中间节点

1
2
3
4
5
6
7
8
9
10
11
12
func getMiddle<T>(_ list: LinkedList<T>) -> Node<T>? {
  	//两个步长差一倍，这样快的遍历到终点，慢的刚好到中间
    var fast = list.head
    var slow = list.head

    while let nextFast = fast?.next {
        fast = nextFast.next
        slow = slow?.next
    }

    return slow
}

反转链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
extension LinkedList {
    // 不断的分割链表，从头部开始，下一步时把之前分割的节点拼接在新的节点之后。
    // 如此遍历到底，就实现了逆序。
    // 核心思路：把每个节点的前节点变成后节点，同时通过遍历时分割成2~3个分段。
    mutating func reverse() {
        tail = head

        var current = head?.next
        //  临时存储逆序的链表
        var prev = head
        prev?.next = nil

        while current != nil {
            let next = current?.next
            current?.next = prev
            prev = current
            current = next
        }

        head = prev
    }
}

合并两个已经排序好的链表

例如：

1
2
3
4
5
// list1 1 -> 4 -> 10 -> 11

// list2 -1 -> 2 -> 3 -> 6

// merged list -1 -> 1 -> 2 -> 3 -> 4 -> 6 -> 10 -> 11
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
func mergeSorted<T: Comparable>(_ left: LinkedList<T>,
                                _ right: LinkedList<T>) -> LinkedList<T> {
    guard !left.isEmpty else {
        return right
    }

    guard !right.isEmpty else {
        return left
    }

    // 定义新的链表的首尾
    var newHead: Node<T>?
    var tail: Node<T>?

    // 原有链表的游标，后面以此遍历
    var currentLeft = left.head
    var currentRight = right.head

    // 初始设置
    if let leftNode = currentLeft, let rightNode = currentRight {
        if leftNode.value < rightNode.value {
            newHead = leftNode
            currentLeft = leftNode.next
        } else {
            newHead = rightNode
            currentRight = rightNode.next
        }
        tail = newHead
    }

    // 遍历
    while let leftNode = currentLeft, let rightNode = currentRight {
        if leftNode.value < rightNode.value {
            tail?.next = leftNode
            currentLeft = leftNode.next
        } else {
            tail?.next = rightNode
            currentRight = rightNode.next
        }
        tail = tail?.next
    }

    if let leftNode = currentLeft {
        tail?.next = leftNode
    }

    if let rightNode = currentRight {
        tail?.next = rightNode
    }

    // 处理新的链表的首尾
    var list = LinkedList<T>()

    list.head = newHead
    // 找到真的尾部节点
    list.tail = {
        while let next = tail?.next {
            tail = next
        }
        return tail
    }()

    return list
}

创建一个从链表中删除所有特定元素的函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
extension LinkedList where Value: Equatable {
    mutating func removeAll(_ value: Value) {
        // 头部的值相等时单独处理
        while let head = self.head, head.value == value {
            self.head = head.next
        }

        var current = head?.next
        var prev = head

        // 遍历
        while let currentNode = current {
            guard currentNode.value != value else {
                prev?.next = currentNode.next
                current = prev?.next
                continue
            }

            prev = current
            current = current?.next
        }

        tail = prev
    }
}

在时间复杂度上优化，所以一般都是2~3个临时变量（牺牲一点空间复杂度）。相当于让更多人协同做一件事情，肯定更快。但是如果是资源有限的时候，比如说雇人做事，总的成本不一定会减少。但是通常情况下，电脑的内存容量是既定的，而且够用的情况下，就要优化时间复杂度，不用吝惜内存。

第六章：栈

栈无处不在。 以下是您要栈的一些常见示例：

  • 薄煎饼
  • 书籍
  • 纸张

在概念上，栈数据结构与物理栈相同。 将项目添加到栈时，将其放在栈顶部。 从栈中删除项目时，始终会删除最顶层的项目。

栈的操作

栈的操作只有两个：

  1. push：将元素添加到栈顶部。
  2. pop：删除栈的顶部元素。

这意味着您只能在数据结构的一侧添加或删除元素。在计算机科学中，栈被称为LIFO（后进先出）数据结构。最后推入的元素是第一个被弹出的元素。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
//泛型Element为存储的元素
public struct Stack<Element> {

  //内部为数组存储所有元素
  private var storage: [Element] = []

  public init() { }

  public init(_ elements: [Element]) {
    storage = elements
  }

  public mutating func push(_ element: Element) {
    storage.append(element)
  }

  @discardableResult
  public mutating func pop() -> Element? {
    return storage.popLast()
  }

  public func peek() -> Element? {
    return storage.last
  }

  public var isEmpty: Bool {
    return peek() == nil
  }
}

extension Stack: CustomStringConvertible {
  public var description: String {
    let topDivider = "----top----\n"
    let bottomDivider = "\n-----------"

    let stackElements = storage
      .map { "\($0)" }
      .reversed()
      .joined(separator: "\n")
    return topDivider + stackElements + bottomDivider
  }
}

extension Stack: ExpressibleByArrayLiteral {
  public init(arrayLiteral elements: Element...) {
    storage = elements
  }
}

你可能想知道是否可以为栈采用Swift集合协议。栈的目的是限制访问数据的方式的数量，并采用诸如Collection之类的协议将通过迭代器和下标公开所有元素来违背此目标。在这种情况下，少即是多！

第七章：栈挑战

逆序打印链表，但是不能用递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
let list: LinkedList<Int> = {
  var list = LinkedList<Int>()
  list.push(3)
  list.push(2)
  list.push(1)
  return list
}()

func printInReverse<T>(_ list: LinkedList<T>) {
  var current = list.head
  var stack = Stack<T>()
  
  while let node = current {
    stack.push(node.value)
    current = node.next
  }
  
  while let value = stack.pop() {
    print(value)
  }
}

printInReverse(list)

检查括号的匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
var testString1 = "h((e))llo(world)()"
var testString2 = "(hello world"

func checkParentheses(_ string: String) -> Bool {
  var stack = Stack<Character>()
  
  for character in string {
    if character == "(" {
      stack.push(character)
    } else if character == ")" {
      if stack.isEmpty {
        return false
      } else {
        stack.pop()
      }
    }
  }
  return stack.isEmpty
}

checkParentheses(testString1)
checkParentheses(testString2)

第八章：队列

我们都熟悉排队，无论是买票还是排队打印。

队列使用FIFO或先进先出顺序，这意味着添加的第一个元素将始终是第一个被删除的元素。当您需要维护元素的顺序以便稍后处理时，队列很方便。

定义

让我们先确定队列的协议：

1
2
3
4
5
6
7
8
9
10
public protocol Queue {
  
  associatedtype Element
  ///在队列后面插入一个元素。如果操作成功，则返回true。
  mutating func enqueue(_ element: Element) -> Bool
  ///删除队列前面的元素并将其返回。
  mutating func dequeue() -> Element?
  var isEmpty: Bool { get }
  var peek: Element? { get }
}

在以下部分中，将以四种不同的方式创建队列：

  1. 数组
  2. 双向列表
  3. 环形缓冲区
  4. 双栈

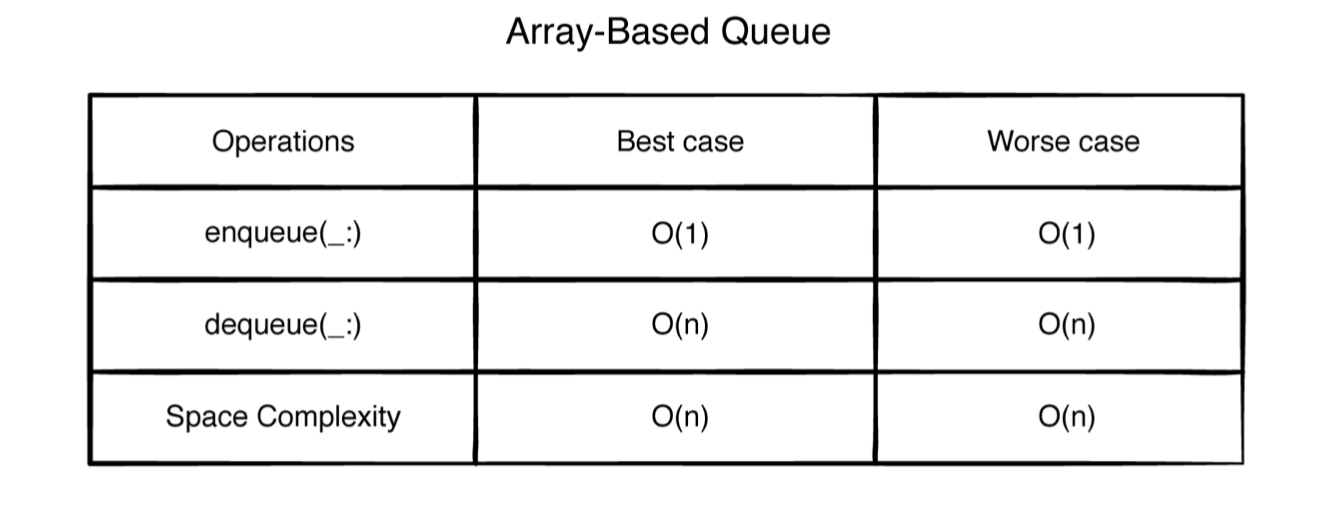
用数组来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public struct QueueArray<T>: Queue {
  
  private var array: [T] = []
  public init() {}

  public var isEmpty: Bool {
    return array.isEmpty
  }
  
  public var peek: T? {
    return array.first
  }
  
  public mutating func enqueue(_ element: T) -> Bool {
    array.append(element)
    return true
  }
  
  public mutating func dequeue() -> T? {
    return isEmpty ? nil : array.removeFirst()
  }
}

extension QueueArray: CustomStringConvertible {
  
  public var description: String {
    return String(describing: array)
  }
}

var queue = QueueArray<String>()
queue.enqueue("Ray")
queue.enqueue("Brian")
queue.enqueue("Eric")
queue
queue.dequeue()
queue
queue.peek
优缺点
image-20190912160423263

很明显只有enqueue是O(1)，其他都是O(n)。

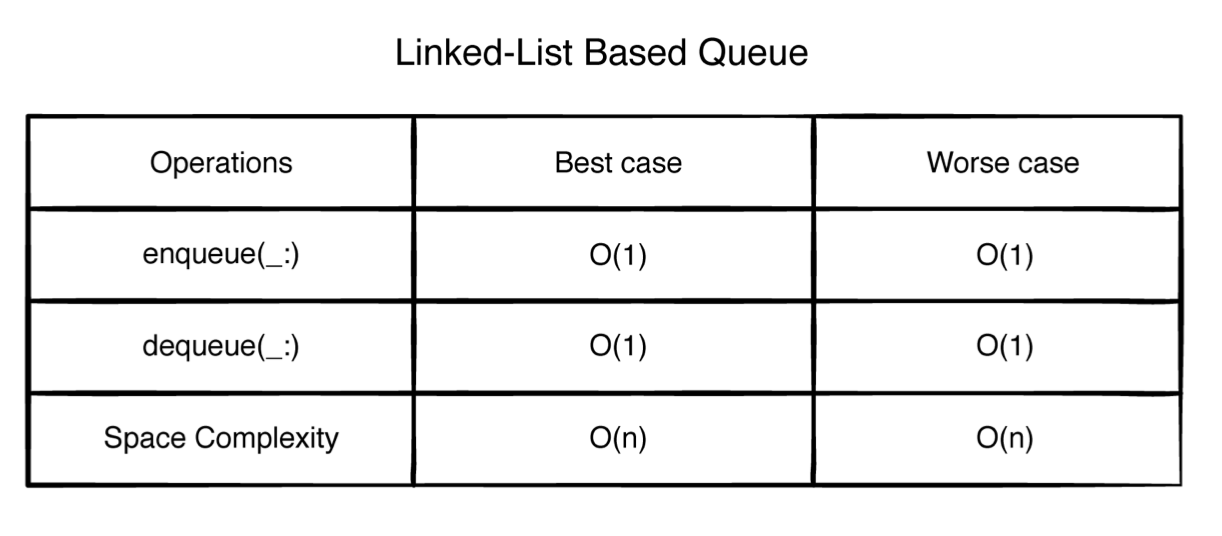
用双向链表来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
public class QueueLinkedList<T>: Queue {
  
  private var list = DoublyLinkedList<T>()
  public init() {}

  public func enqueue(_ element: T) -> Bool {
    list.append(element)
    return true
  }
  
  public func dequeue() -> T? {
    guard !list.isEmpty, let element = list.first else {
      return nil
    }
    return list.remove(element)
  }
  
  public var peek: T? {
    return list.first?.value
  }
  
  public var isEmpty: Bool {
    return list.isEmpty
  }
}

extension QueueLinkedList: CustomStringConvertible {
  
  public var description: String {
    return String(describing: list)
  }
}

var queue = QueueLinkedList<String>()
queue.enqueue("Ray")
queue.enqueue("Brian")
queue.enqueue("Eric")
queue
queue.dequeue()
queue
queue.peek

// MARK: - DoublyLinkedList

public class Node<T> {
  
  public var value: T
  public var next: Node<T>?
  public var previous: Node<T>?
  
  public init(value: T) {
    self.value = value
  }
}

extension Node: CustomStringConvertible {
  
  public var description: String {
    return String(describing: value)
  }
}

public class DoublyLinkedList<T> {
  
  private var head: Node<T>?
  private var tail: Node<T>?
  
  public init() { }
  
  public var isEmpty: Bool {
    return head == nil
  }
  
  public var first: Node<T>? {
    return head
  }
  
  public func append(_ value: T) {
    let newNode = Node(value: value)
    
    guard let tailNode = tail else {
      head = newNode
      tail = newNode
      return
    }
    
    newNode.previous = tailNode
    tailNode.next = newNode
    tail = newNode
  }
  
  public func remove(_ node: Node<T>) -> T {
    let prev = node.previous
    let next = node.next
    
    if let prev = prev {
      prev.next = next
    } else {
      head = next
    }
    
    next?.previous = prev
    
    if next == nil {
      tail = prev
    }
    
    node.previous = nil
    node.next = nil
    
    return node.value
  }
}

extension DoublyLinkedList: CustomStringConvertible {
  
  public var description: String {
    var string = ""
    var current = head
    while let node = current {
      string.append("\(node.value) -> ")
      current = node.next
    }
    return string + "end"
  }
}

public class LinkedListIterator<T>: IteratorProtocol {
  
  private var current: Node<T>?
  
  init(node: Node<T>?) {
    current = node
  }
  
  public func next() -> Node<T>? {
    defer { current = current?.next }
    return current
  }
}

extension DoublyLinkedList: Sequence {
  
  public func makeIterator() -> LinkedListIterator<T> {
    return LinkedListIterator(node: head)
  }
}
优缺点image-20190912161101034

出来空间复杂度是O(n)，其他的都是O(1)。

双向列表的主要弱点在表中并不明显。尽管有O(1)的性能，但它的开销很高。每个元素都必须有额外的存储空间用于前向和后向引用。而且，每次创建新元素时，都需要相对昂贵的动态分配。相比之下，数组进行批量分配，速度更快。

用环形缓冲区来实现

环形缓冲区，也称为循环缓冲区，是固定大小的阵列。当最终没有更多项目需要删除时，这种数据结构战略性地包含在开头。

详见：[https://github.com/raywenderlich/swift-algorithm-club/tree/master/Ring%20Buffer](https://github.com/raywenderlich/swift-algorithm-club/tree/master/Ring Buffer)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
public struct QueueRingBuffer<T>: Queue {
  
  private var ringBuffer: RingBuffer<T>
  
  public init(count: Int) {
    ringBuffer = RingBuffer<T>(count: count)
  }
  
  public var isEmpty: Bool {
    return ringBuffer.isEmpty
  }
  
  public var peek: T? {
    return ringBuffer.first
  }
  
  public mutating func enqueue(_ element: T) -> Bool {
    return ringBuffer.write(element)
  }
  
  public mutating func dequeue() -> T? {
    return isEmpty ? nil : ringBuffer.read()
  }
}

extension QueueRingBuffer: CustomStringConvertible {
  
  public var description: String {
    return String(describing: ringBuffer)
  }
}

var queue = QueueRingBuffer<String>(count: 10)
queue.enqueue("Ray")
queue.enqueue("Brian")
queue.enqueue("Eric")
queue
queue.dequeue()
queue
queue.peek

// MARK: - RingBuffer

public struct RingBuffer<T> {
  
  private var array: [T?]
  private var readIndex = 0
  private var writeIndex = 0
  
  public init(count: Int) {
    array = Array<T?>(repeating: nil, count: count)
  }
  
  public var first: T? {
    return array[readIndex]
  }
  
  public mutating func write(_ element: T) -> Bool {
    if !isFull {
      array[writeIndex % array.count] = element
      writeIndex += 1
      return true
    } else {
      return false
    }
  }
  
  public mutating func read() -> T? {
    if !isEmpty {
      let element = array[readIndex % array.count]
      readIndex += 1
      return element
    } else {
      return nil
    }
  }
  
  private var availableSpaceForReading: Int {
    return writeIndex - readIndex
  }
  
  public var isEmpty: Bool {
    return availableSpaceForReading == 0
  }
  
  private var availableSpaceForWriting: Int {
    return array.count - availableSpaceForReading
  }
  
  public var isFull: Bool {
    return availableSpaceForWriting == 0
  }
}

extension RingBuffer: CustomStringConvertible {
  public var description: String {
    let values = (0..<availableSpaceForReading).map {
      String(describing: array[($0 + readIndex) % array.count]!)
    }
    return "[" + values.joined(separator: ", ") + "]"
  }
}
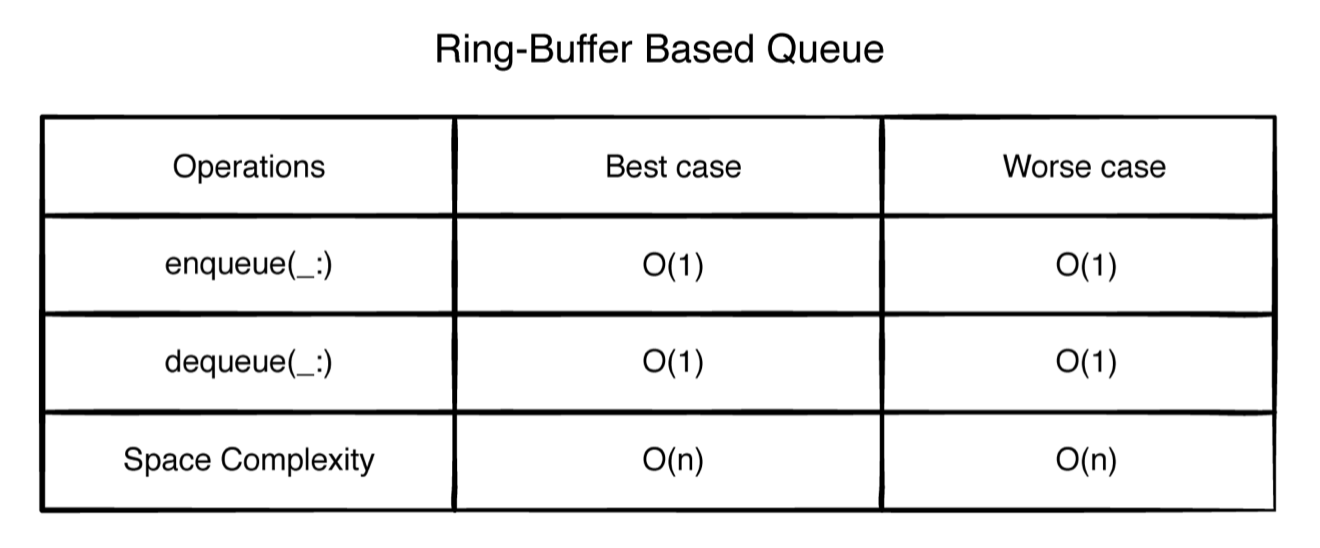
优缺点

image-20190912162139308

基于环缓冲区的队列具有与链表实现相同的入队和出队时间复杂度。唯一的区别是空间复杂性。环形缓冲区具有固定大小，这意味着入队可能会失败。

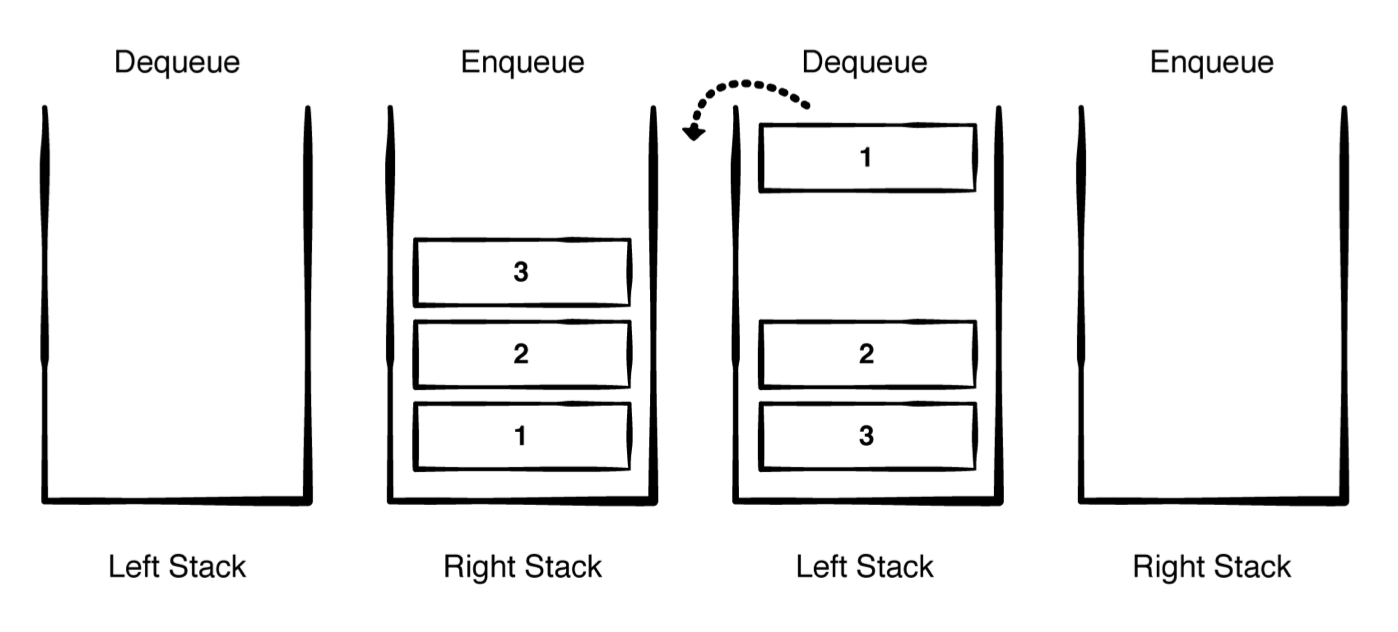
用双栈来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public struct QueueStack<T> : Queue {
  
  private var leftStack: [T] = []
  private var rightStack: [T] = []
  public init() {}
  
  public var isEmpty: Bool {
    return leftStack.isEmpty && rightStack.isEmpty
  }
  
  public var peek: T? {
    return !leftStack.isEmpty ? leftStack.last : rightStack.first
  }
  
  public mutating func enqueue(_ element: T) -> Bool {
    rightStack.append(element)
    return true
  }
  
  public mutating func dequeue() -> T? {
    if leftStack.isEmpty {
      leftStack = rightStack.reversed()
      rightStack.removeAll()
    }
    return leftStack.popLast()
  }
}

extension QueueStack: CustomStringConvertible {
  
  public var description: String {
    let printList = leftStack.reversed() + rightStack
    return String(describing: printList)
  }
}

var queue = QueueStack<String>()
queue.enqueue("Ray")
queue.enqueue("Brian")
queue.enqueue("Eric")
queue
queue.dequeue()
queue
queue.peek

出队：image-20190912162831309

入队：

![image-20190912162918069](/Users/will/Library/Application Support/typora-user-images/image-20190912162918069.png)

优缺点
![image-20190912163001741](/Users/will/Library/Application Support/typora-user-images/image-20190912163001741.png)

与基于数组的实现相比，通过利用两个堆栈，您可以将dequeue(_ :)转换为分摊的O(1)操作。

此外，您的双栈实现是完全动态的，并且没有基于环形缓冲区的队列实现所具有的固定大小限制。

总结

  • 队列采用FIFO策略，首先必须先删除添加的元素。

  • Enqueue将元素插入队列的后面。

  • Dequeue删除队列前面的元素。

  • 数组中的元素在连续的内存块中布局，而链表中的元素更加分散，可能存在缓存未命中。

  • 基于环路缓冲区队列的实现适用于具有固定大小的队列。

  • 与其他数据结构相比，利用两个栈可以将出列dequeue(_ :)时间复杂度提高到摊销的O(1)操作。

  • 双栈实现在空间复杂度方面击败了链表。

第九章：队列挑战

解释栈和队列之间的区别

为每个数据结构提供两个实际示例。

画逐步图表

演示四种实现时，每一步对队列的有影响。

如队列为：”SWIFT”

1
2
3
4
5
6
7
enqueue("R") 
enqueue("O") 
dequeue() 
enqueue("C") 
dequeue() 
dequeue() 
enqueue("K")

给队列添加next协议

用来大富翁游戏，指派下一个玩家

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public protocol BoardGameManager {
  associatedtype Player
  mutating func nextPlayer() -> Player?
}

extension QueueArray: BoardGameManager {
    
  public typealias Player = T
  
  public mutating func nextPlayer() -> T? {
    guard let person = dequeue() else {
      return nil
    }
    enqueue(person)
    return person
  }
}

逆序排列队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
extension QueueArray {
    
  func reversed() -> QueueArray {
    var queue = self
    var stack = Stack<T>()
    while let element = queue.dequeue() {
      stack.push(element)
    }
    while let element = stack.pop() {
      queue.enqueue(element)
    }
    return queue
  }
}